DSE數學公式繁多,如果想更好地理解和使用公式,那就需要加以例子一起學習。雖然市面上有不少數學應用程式可以一次過溫習所有數學公式,但它們缺少了相關的應用例子及數學題目。因此,GJ Math為各位DSE考生整理了數學公式大全,分為上下兩集,並附上2022至2023年度數學DSE卷二的例子。希望大家在背公式的同時,也有相應的DSE題目附助,幫助理解和應用公式。
數學公式- Logarithm對數
| log a + log b = log ab log a – log b = log \frac{a}{b} log a^n = nlog a log_{b} a = \frac{log_{c}a}{log_{c}b} , for any c > 0, c ≠ 1 log_{a}1 = 0 log_{a}a = 1 |
數學公式適用題目:
2022 DSE P2 Q32
已知 log_{a}y 為 x 的線性函數,其中 0 < a < 1。該線性函數的圖像在垂直軸上的截距及在水平軸上的截距分別為6及3。若 y = mn^x ,則下列何者正確?
It is given that log_{a}y is a linear function of x , where 0 < a < 1 . The intercepts on the vertical axis and on the horizontal axis of the graph of the linear function are 6 and 3 respectively. If y = mn^x , which of the following is/are true?
I. m<1
II. n<1
III. mn^3=1
A. 只有 I (I only)
B. 只有 II (II only)
C. 只有 I 及 III (I and III only)
D. 只有 II 及 III (II and III only)
答案:C
2022 DSE P2 Q33
若 log_{4}y = 2x-1 及 (log_{4}y)^2= 20x-31,則 log_{2}y=
If log_{4}y = 2x-1 and (log_{4}y)^2= 20x-31 , then log_{2}y=
A. 1或2。 (1 or 2)
B. 2或4。 (2 or 4)
C. 3或7。 (3 or 7)
D. 6或14。 (6 or 14)
答案:D
數學公式- Deductive Geometry 演繹幾何定理
幾何定理 (Geometry)
| Angles 角度 | Properties 特性 |
| a + b = 180° adj. ∠s on st. line 直線上的鄰角 | |
| a + b + c = 360° ∠s at a pt. 同頂角 | |
| a = b vert. opp. ∠s 對頂角 | |
| a + b + c = 180° ∠ sum of Δ Δ內角和 | |
| a + b = c_1 ext. ∠ of Δ Δ外角 *快捷版,可不記 |
角與平行線 (Angles and Parallel Lines)
| Situation 情況 | Properties 特性 | Prove 證明 |
| If AB // CD, then a = b corr. ∠s, AB // CD 同位角,AB // CD | If a = b, then AB // CD corr. ∠s equal 同位角相等 | |
| If AB //CD, then a = b alt. ∠s, AB // CD 錯角,AB // CD | If a = b, then AB //CD alt. ∠s equal 錯角相等 | |
| If AB // CD, then a + b = 180° int. ∠s, AB // CD 同旁內角,AB //CD | If a + b = 180°, then AB // CD int. ∠s supp. 同旁內角互補 |
凸多邊形的角 (Angles of Convex Polygon)
| Situation 情況 | Properties 特性 |
| a_1 + a_2 + a_3 + … + a_n = (n − 2) × 180° ∠ sum of polygon 多邊形的內角和 → Regular 正多邊形 Each interior angle 每隻內角 = \frac{(n − 2) × 180°}{n} | |
| x_1 + x_2 + x_3 + … + x_n = 360° sum of ext. ∠s of polygon 多邊形的外角和 → Regular 正多邊形 Each exterior angle 每隻外角= \frac{360º}{n} |
全等三角形及相似三角形 (Congruent Triangles and Similar Triangles)
| Congruent Triangles 全等三角形 (P.S. congruent 全等 Δ 係 similar 相似 Δ其中一種) | Similar Triangles 相似三角形 |
| 三邊成比例 | |
| 兩邊成比例且夾角 | |
| / | |
| / |
If ΔABC ≅ΔXYZ, then ∠A = ∠X, ∠B = ∠Y, ∠C = ∠Z (corr. ∠s, ≅Δs) 全等三角形對應角 AB = XY, BC = YZ, CA = ZX (corr. sides, ≅Δs) |
If ΔABC ~ ΔXYZ, then ∠A = ∠X, ∠B = ∠Y, ∠C = ∠Z (corr. ∠s, ≅Δs) \frac{AB}{XY} = \frac{BC}{YZ} = \frac{CA}{ZX} (corr. sides, ~Δs) 相似三角形對應邊 |
四邊形的特性 (Properties of quadrilateral)
| Situation 情況 | Properties 特性 | Prove 證明 |
| ∠P + ∠Q = 180° ∠R + ∠S = 180º Prop. of trapezium 梯形性質 | / | |
| 90º + all prop. of //gram 所有平行四邊形性質 | / | |
| AD = BC & AB = DC ∠A = ∠C & ∠B = ∠D AO = CO & BO = DO AD = BC & AD // BC prop. of //gram 平行四邊形性質 | opp. sides equal 對邊相等 opp. ∠s equal 對角相等 diags. bisect each other 對角線互相平分 2 sides equal and // 一組對邊相等且平行 | |
| diagonals are ⊥ 對角線互相垂直 4 sides equal 四邊相等 Interiors are bisected by diagonals 對角線平分頂角 + all prop. of //gram 所有平行四邊形性質 Properties of rhombus 菱形性質 | / |
三角形性質 (The Properties of Triangle)
| Triangle 三角形 | Properties 性質 |
| Right-angled triangle 直角三角形 | 🌟見到直角唔係畢氏定理就係sin/cos/tan sin θ = \frac{opp.對}{hyp.斜} = \frac{a}{c} cos θ = \frac{adj.鄰}{hyp.斜} = \frac{b}{c} tan θ = \frac{opp.對}{adj.鄰} = \frac{a}{b} a^2 + b^2 = c^2 (pyth. Them. 畢氏定理) If a^2 + b^2 = c^2, then ∠C = 90º (Converse of Pyth. Thm. 畢氏定理逆定理) |
| Isosceles triangle 等腰三角形 | If AB = AC, then ∠ABC = ∠ACB (base ∠s, isos. Δ 等腰Δ底角) If ∠ABC = ∠ACB, then AB = AC (sides opp. equal ∠s 等角對邊相等) If ΔABC is an isos. Δ, then AD ⊥ BC & BD = DC & ∠BAD = ∠CAD (prop. of isos. Δ 等腰Δ性質) |
| Equilateral Triangle 等邊三角形 | If AB = BC = CA, then ∠A, ∠B, ∠C = 60º, vice versa (prop. of equil. Δ 等邊Δ性質) |
中點定理及截線定理 (Mid-point Theorem and Intercept Theorem)
| Situation 情況 | Theorem 定理 |
| If AE = EB and AF = FC, then EF // BC & EF = \frac{1}{2}BC (Mid-pt. theorem 中點定理) If AE = EB and EF // BC, then AF = FC (intercept theorem 截線定理) | |
| If AC = CE and AB // CD // EF, then BD = DF (intercept theorem 截線定理) |
三角不等式 (Triangle Inequality)
| a + b > c b + c > a c + a > b |
正弦餘弦公式 (Sine Consine Formula)
| Sine formula 正弦公式 (2邊2角): |
| \frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} |
| Consine formula 餘弦公式 (3邊1角): |
| c^2 = a^2 + b^2 − 2abcosC |
三角形的中心 (Center Formula)
| 內心-角平分線 | 外心-垂直平分線 |
| 垂心-高線 | 形心-中線 |
對稱 (Symmetry)
| Solid 立體 | Plane of reflection 反射平面 | Axis of rotation 旋轉軸 |
| Cube 立方體 | 9 | 13 |
| Tetrahedron 四面體 | 6 | 7 |
| Regular octahedron 正八面體 | 9 | 13 |
| Axis of symmetry of n-sided regular polygon 正n邊形的對稱數= n Order of rotational symmetry of n-sided regular polygon 正n邊形的旋轉折式數目 = n Number of diagonals of n-sided polygon 正n邊形的對角線 = \frac{n(n − 3)}{2} |
數學公式適用題目:
2023 DSE P2 Q18
根據圖中所示,下列何者必為正確?
According to the figure, which of the following must be true?
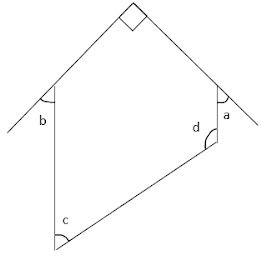
I. a+b=90º
II. c+d=180º
III. a+b+c=d
A. 只有 I 及 II (I and II only)
B. 只有 I 及 III (I and III only)
C. 只有 II 及 III (II and III only)
D. I、II 及 III (I, II and III)
答案:A
2023 DSE P2 Q19
已知ABCD為一菱形。將AC與BD的交點記為E。下列何者必為正確?
It is given that ABCD is a rhombus. Denote the point of intersection of AC and BD by E. Which of the following must be true?
I. AE = BE
II. \frac{AE}{AC} = \frac{BE}{BD}
III. AE^2+BE^2=CD^2
A. 只有 I 及 II (I and II only)
B. 只有 I 及 III (I and III only)
C. 只有 II 及 III (II and III only)
D. I、II 及 III (I, II and III)
答案:C
數學公式-Variations 變分
| Direct variations 正變 (未知數寫分子): If y varies directly as x, then y = kx for some non-zero constant k. 若y 隨x而正變,則y = kx,其中k為非零常數。 |
| Inverse variations 反變 (未知數寫分母): If y varies inversely as x, then y = \frac{k}{x} for some non-zero constant k. 若 y 隨 x反變,則y = \frac{k}{x} ,其中k為非零常數。 |
| Joint variations 聯變: If z varies inversely as x and y, then z = kxy for some non-zero constant k. 若z 隨x 及y聯變, 則z = kxy,其中k為非零常數。 |
| Partial variations 部分變: → If z is partly constant and partly varies directly as x, then z = k_{1} + k_{2}x for some non-zero constant k. 若z 部分為常數及部分隨x正變, 則z = k_{1} + k_{2}x,其中k為非零常數。 → If z partly varies directly as x and partly varies inversely as y, then z = k_{1}x + \frac{k_{2}}{y} for some non-zero constant k. 若z 部分隨x 正變及部分隨y反變, 則z = k_{1} + \frac{k_{2}}{y},其中k為非零常數。 |
數學公式適用題目:
2022 DSE P2 Q13
若 u 隨 v 的平方根正變且隨 w 反變,則下列何者正確?
If u varies directly as the square root of v and inversely as w , which of the following are true?
I. u^2 隨 v 正變且隨 w 的平方反變。
u^2 varies directly as v and inversely as the square of w.
II. v 隨 w 正變且隨 u 的平方根反變。
v varies directly as w and inversely as the square root of u.
III. w 隨 v 的平方根正變且隨 u 反變。
w varies directly as the square root of v and inversely as u.
A. 只有 I 及 II (I and II only)
B. 只有 I 及 III (I and III only)
C. 只有 II 及 III (II and III only)
D. I、II 及 III (I, II and III)
答案:B
2023 DSE P2 Q13
已知 z 隨 x 的平方及 y 的立方根正變。當 x=12 及 y=64 時,z=36。當 x=16 及 y=729 時,z=
It is given that z varies as the square of x and the cube root of y. When x=12 and y=64, z=36. When x=16 and y=729, z=
A. 108
B. 144
C. 162
D. 216
答案:B
大家記得留意數學公式大全(下集),我們將會講述有關多項式、複數、二次方程、率與比、誤差、恆等、百分比、二次函數以及整數指數律的數學公式!這些公式是DSE數學考試中非常重要的一部分,掌握它們可以幫助學生更好地應對考試,提高自己的數學成績和能力。
如對於DSE數學有任何問題,如私人補習、網上補習等,或者想知道更多關於DSE的資訊,歡迎Follow「學博教育中心 Learn Smart Education」 Facebook page 和 IG,以及 瀏覽 GJ MATHS 的 數學資源網站 及 IG,入面有齊所有你想知道和你需要知道的DSE資訊,助你全力應戰DSE!!