大家是否曾經好奇，我們辛辛苦苦學習的數學理論是由誰發明出來？這些聰明數學家生平和經歷是怎樣的呢？今天，我們不僅會分享『畢氏定理之父』畢達哥拉斯的故事，還會探索其他著名數學家的心路歷程和理論成就。讓我們一起走進數學家的世界，探索他們的故事，感受數學家們的智慧和創造力吧！

數學家：畢達哥拉斯（Pythagoras）

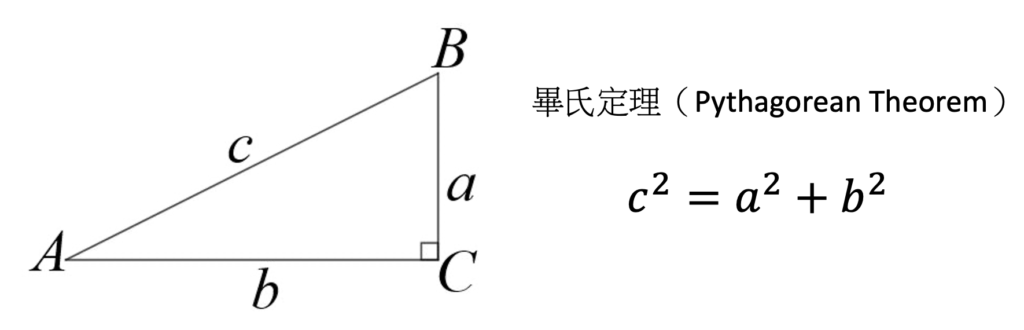
理論：畢氏定理（Pythagorean Theorem）

畢達哥拉斯（Pythagoras）是古希臘最傑出的數學家之一，他的研究對幾何學、數學和哲學的發展產生了深遠的影響。畢達哥拉斯生於公元前570年左右的撒摩斯島（Samos Island），他的父親是一位富有的商人，曾經經營過貿易。年輕時他曾到埃及和巴比倫等地旅行，接觸到當時世界各地的知識和文化，並在巴比倫學習了數學和天文學。

在他的學習過程中，畢達哥拉斯發現了一些重要的數學定理，其中最著名的是畢氏定理（Pythagorean Theorem）。畢氏定理是指在直角三角形中，直角兩邊的平方之和等於斜邊的平方，即 a^2+b^2=c^2。這個定理對於測量和計算三角形的面積和周長非常重要，因此它被廣泛地應用於數學和物理學等領域。數學家畢達哥拉斯主張數學應該建立在嚴謹的公理化基礎上，通過推理和證明來確定數學的真理，這個思想對現代數學的發展有著深遠的影響。

除此之外，畢達哥拉斯還是一位傑出的哲學家和思想家。他的思想和理念對後世的哲學和宗教產生了深遠的影響。他創立了一個以數學為基礎的哲學體系，認為數學是宇宙秩序的基礎，通過數學可以找到萬物的本質和真理。

數學家：卡爾·弗里德里希·高斯 （Johann Carl Friedrich Gauß）

九歲時解開了老師出的「從  1 加到 100」的數學題。

卡爾·弗里德里希·高斯（Carl Friedrich Gauss）是19世紀德國卓越的數學家之一，他的研究和貢獻對數學和科學的發展帶來了革命性的影響。高斯於1777年出生於布倫瑞克（Braunschweig），在貧窮家庭中長大。然而在他的童年時期，他便表現出了非凡的數學才華，九歲時便解決了老師出的「從1加到100」的數學題。

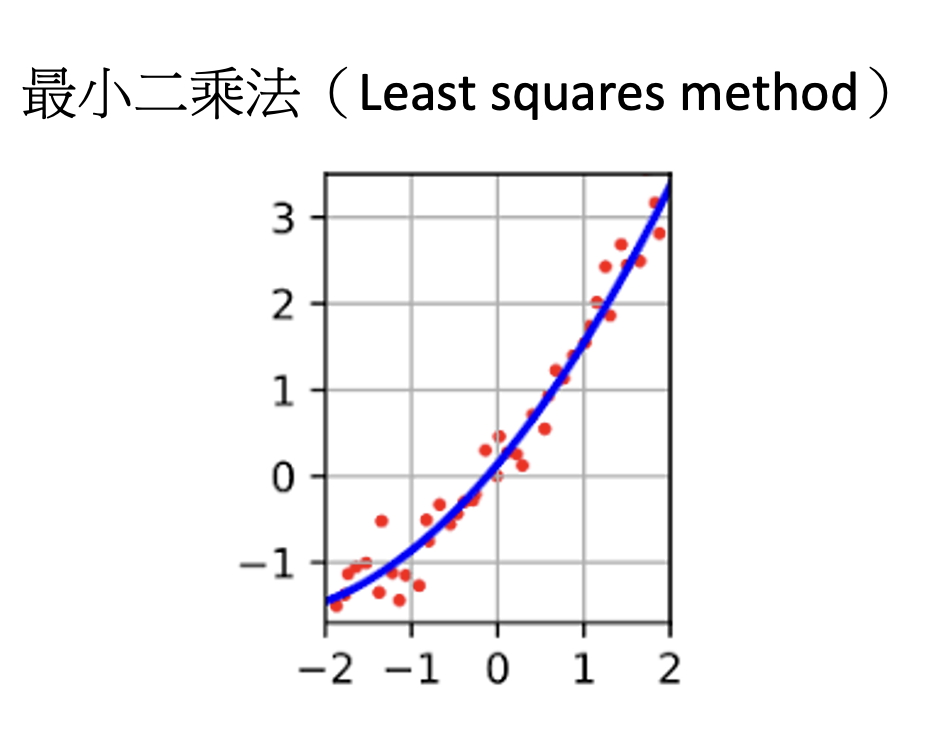
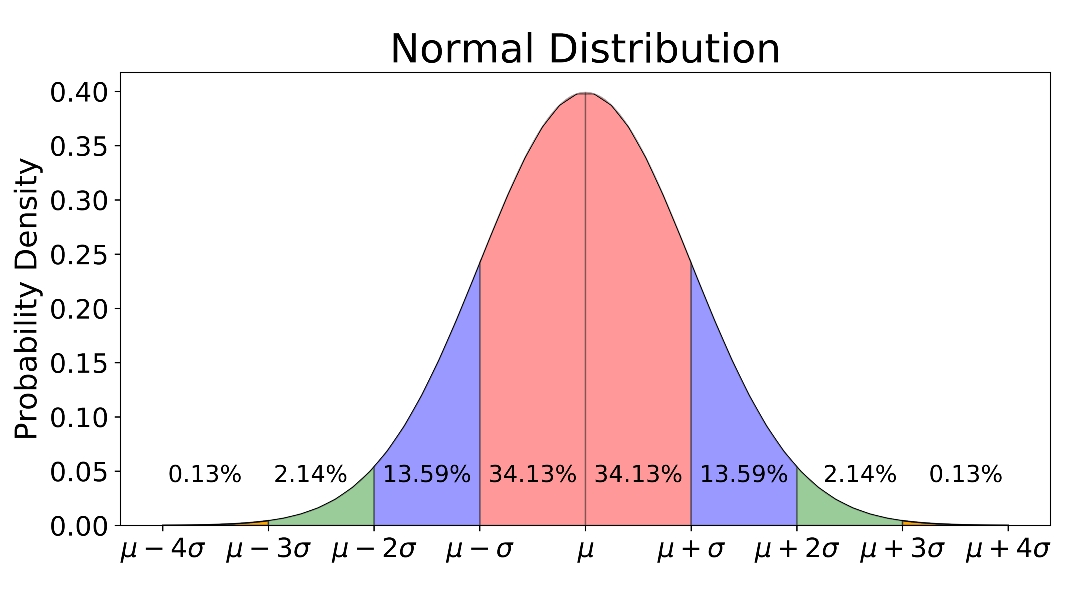
高斯在數學領域做出了許多貢獻，其中最著名的是他發現了最小二乘法（Least squares method），即通過最小化誤差來求解線性方程組（System of linear equations）的方法。他也創建了高斯-約旦消元（Gauss-Jordan Elimination）以簡化線性方程組（System of linear equations）求解過程。此外，數學家高斯還證明了一個代數方程式存在有理根（Rational root）的必要條件，並且發現了一些代數方程式的根式解法。高斯在統計學方面的貢獻也很重要，他發明了正態分布（Normal distribution），這是一種在統計學中廣泛使用的概率分布模型。

此外，數學家高斯還對天文學、物理學、地球科學做出了重要的貢獻。例如，他成功預測了小行星的存在，以及發現了許多有關電磁學和熱力學的重要定律和公式，為這些領域的發展奠定了偉大的基礎。

數學家：艾薩克·牛頓（Isaac Newton）

創建了微積分（Calculus）。

艾薩克·牛頓（Isaac Newton）是17世紀英國傑出的科學家和數學家，他的理論和發現奠定了物理學、天文學、光學、數學等領域的基礎。

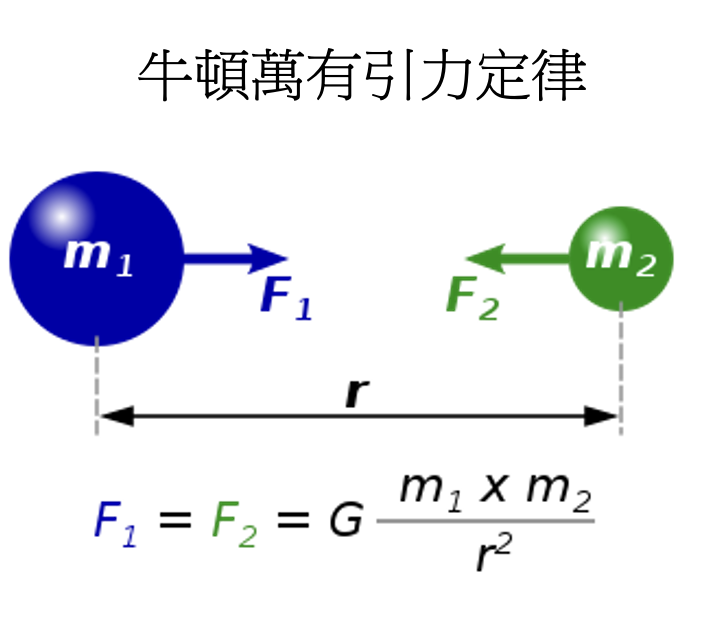
牛頓於1642年12月25日出生於英國林肯郡的一個農民家庭，年幼時表現出了非凡的數學和科學才華。他在劍橋大學學習，後來成為該校的數學教授。在1687年出版的《自然哲學的數學原理》中，牛頓提出了他的三大運動定律（Newton’s Laws of Motion）和萬有引力定律（Newton’s law of universal gravitation），這些成就使他成為現代物理學的奠基人之一。

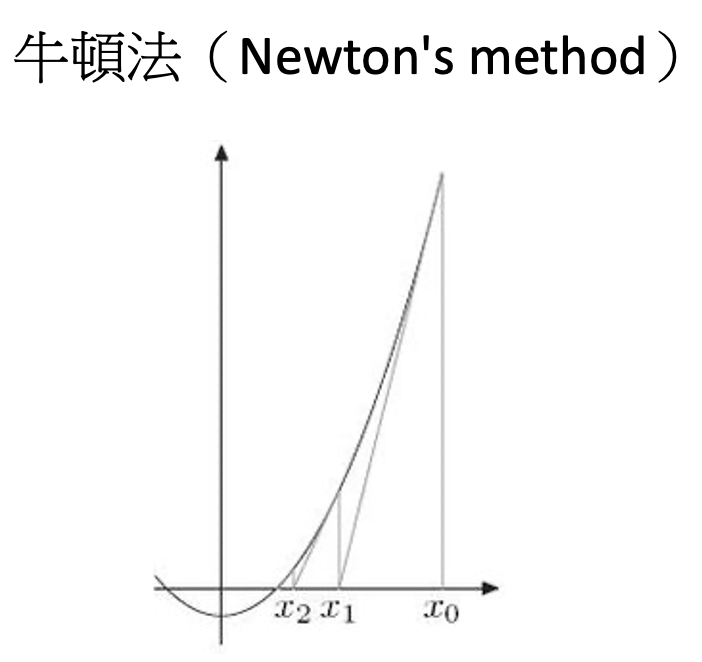
數學家牛頓亦是微積分學的創始人之一，他發現了微積分的基本定理（The fundamental theorem of calculus），即積分（integral）與微分（derivative）具有互逆性（inverse operations），這對微積分學的發展產生了極大的影響。此外，他還發明了牛頓法（Newton’s method），這是一種求解方程的方法，被廣泛應用於現代數學和工程學中。

數學家：阿基米德（Archimedes）

利用「逼近法」（approximation method）算出球表面積、球體積、拋物線、橢圓面積。

阿基米德（Archimedes）是古希臘無與倫比的數學家之一。他生於公元前287年，在希臘的西西里島成長和學習。來自貴族家庭的他接受了優秀的教育，並為數學、物理學、工程學等領域做出了重要貢獻。

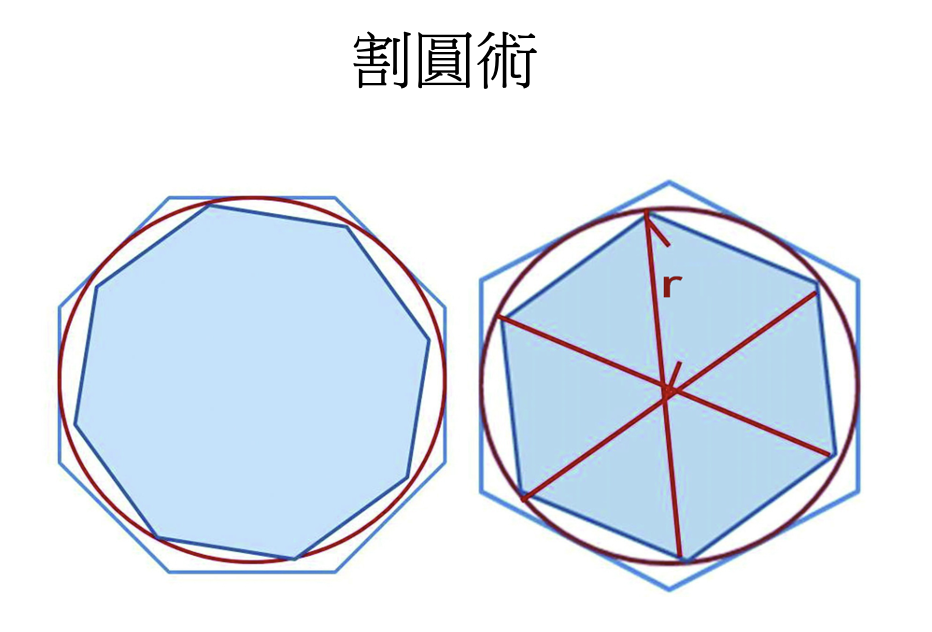
數學家阿基米德發現了許多幾何學定理和數學性質，包括利用「逼近法」（Approximation method）算出球表面積、球體積、拋物線、橢圓面積、利用割圓術計算出圓周率π以及研究出阿基米德螺旋線（Archimedean spiral）等。他還提出許多方法來計算各種幾何圖形的重心，其中包括由一抛物線和其網平行弦線所圍成圖形的重心的方法。

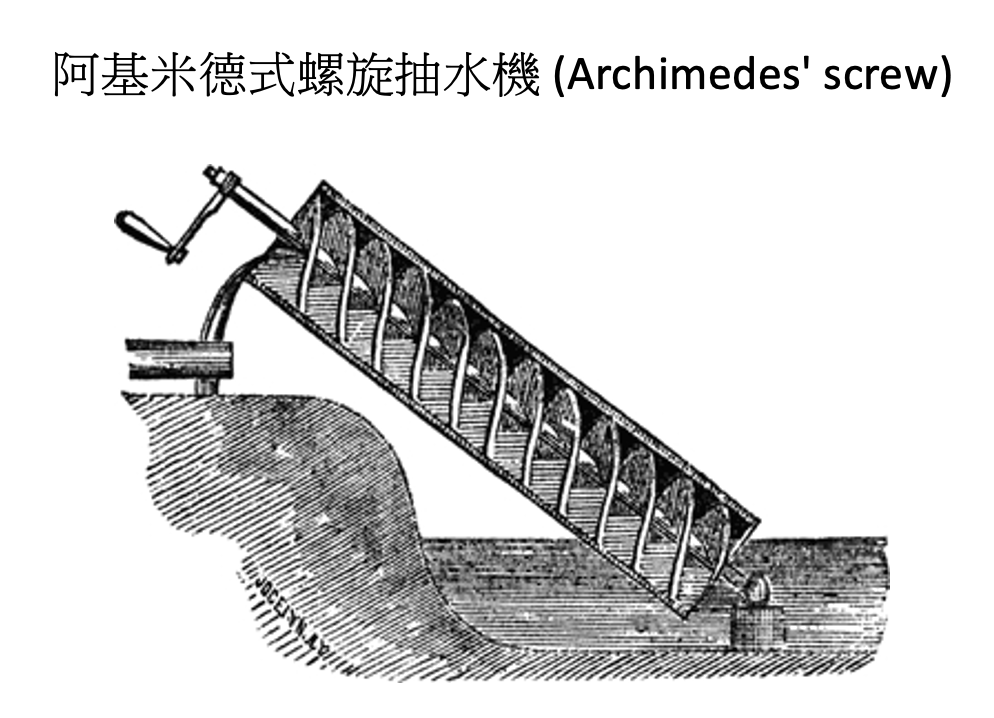
此外，阿基米德對工程學及物理學的發展也非常重要。例如，他提出了阿基米德浮體原理（Archimedes’ principle），描述了物體在液體中浮力的大小和方向。他還設計了一些機械裝置和工具，如阿基米德式螺旋抽水機 (Archimedes’ screw)、阿基米德鏡等，這些設計在古代和現代工程學中都有著廣泛的應用。

數學家：萊昂哈德·歐拉（Leonhard Paul Euler）

發現了歐拉公式（Euler’s formula）及歐拉定理（Euler’s Theorem）。

萊昂哈德·歐拉（Leonhard Paul Euler）是18世紀歐洲其中一位最偉大的數學家之一。歐拉於1707年出生於瑞士巴塞爾，是一個牧師家庭的孩子。歐拉在數學家約翰·伯努利的指導下開始學習數學。儘管在職業生涯中曾多次遭受視力問題和健康問題的困擾，但他仍然保持著高度的生產力和創造力。

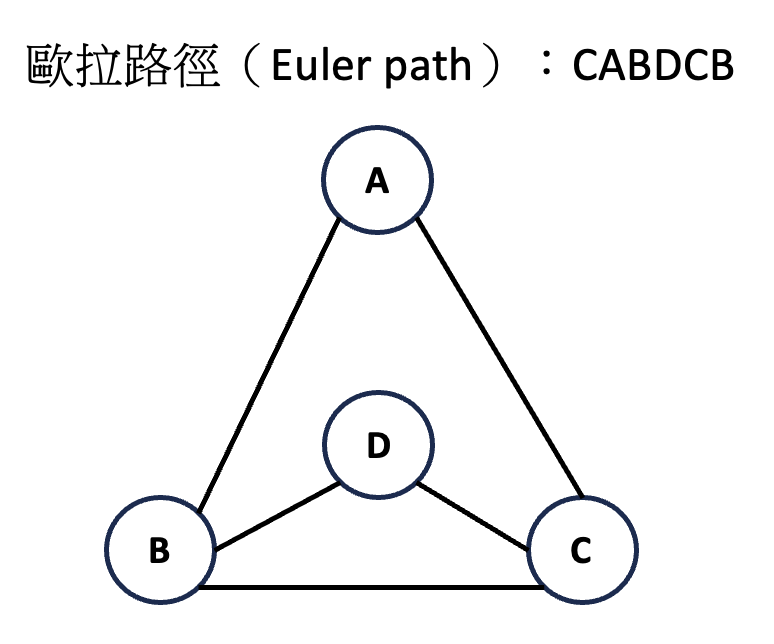
數學家高斯曾經說過：『研究歐拉的著作永遠是瞭解數學的最好方法。』這句話表明了歐拉在數學史上的重要地位。歐拉的數學貢獻包括發現和證明歐拉公式（Euler’s formula）e^{iπ}=-1或e^{iπ}+1=0，其中e代表自然對數的底數，i代表虛數單位。他還提出歐拉定理（Euler’s Theorem）它表明a和n互質時，a^{φ(n)}≡ 1 (mod n)，其中φ(n)表示小於n的正整數中與n互質的數的個數。此外，數學家歐拉也是圖論Graph Theory的奠基人之一，他研究了歐拉路徑（Euler path）及歐拉回路（Euler circuit），並提出了相關的定理和算法。

數學家：伯恩哈德·黎曼（Bernard Riemann）

研究出黎曼幾何學（Riemannian geometry）、黎曼積分（Riemann integral）以及黎曼曲面（Riemann Surface）。

伯恩哈德·黎曼（Bernhard Riemann）是19世紀德國傑出的數學家之一，黎曼於1826年出生於漢諾威王國（今德國下薩克森），是一個牧師家庭的孩子。

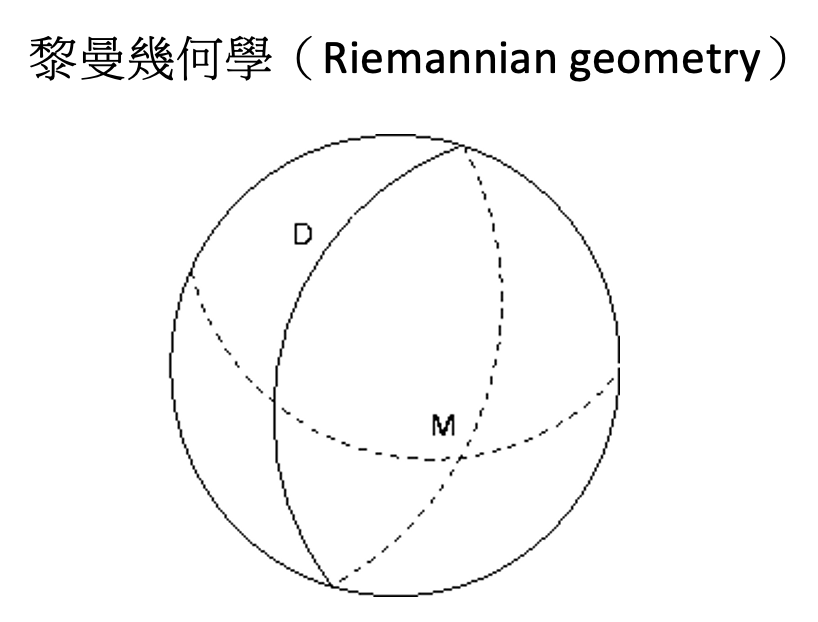
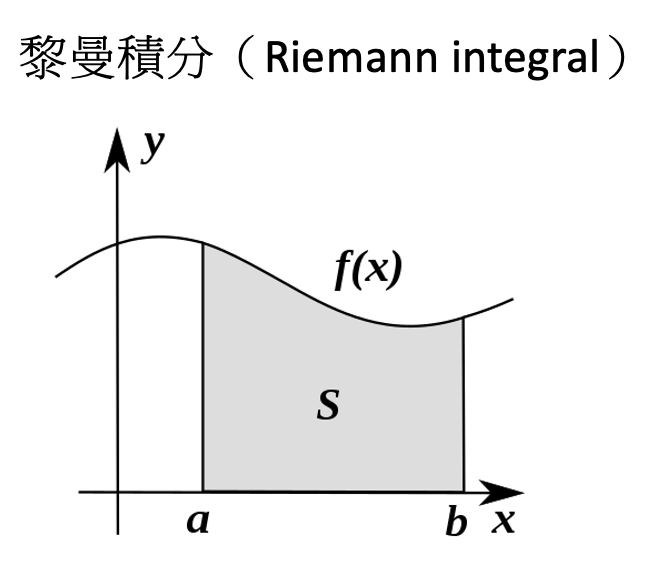
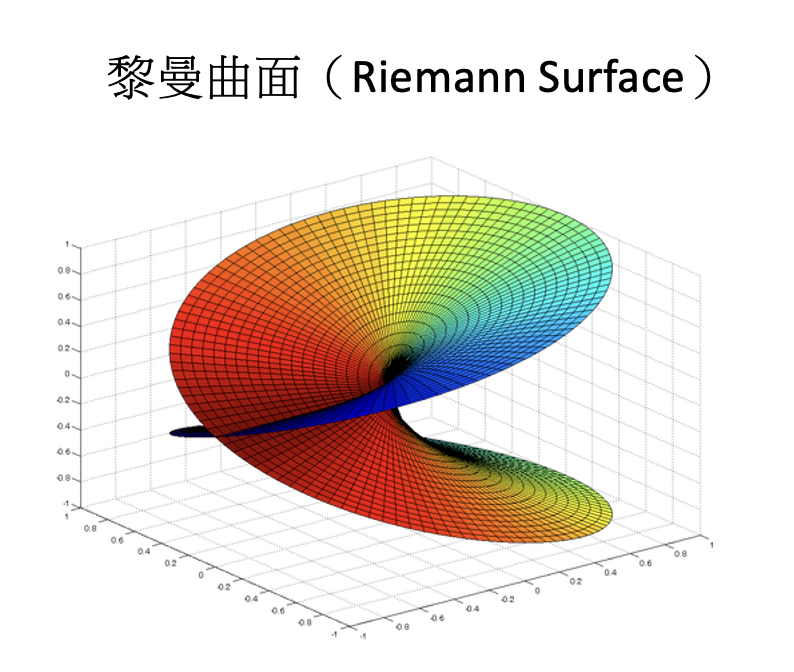
他在高中時代就開始研究數學，後來更發展了黎曼幾何學（Riemannian geometry）、黎曼積分（Riemann integral）、黎曼曲面（Riemann Surface）等重要概念。黎曼幾何被定義為一個相對應的空間中的形式，而不是作為一個平面或曲面中的形式。而黎曼積分就是將積分的定義從有限區間推廣到無限區間，被廣泛應用於分析學和物理學。黎曼曲面則將曲面概念推廣到更高維度的空間中，用於描述多維度的物理學和數學問題。

此外，數學家黎曼還發展了複分析學（Complex analysis）的基礎，並提出了著名的黎曼猜想（Riemann hypothesis），這是一個至今尚未被證明的數學問題，但對數學基礎的研究有著深遠的影響。

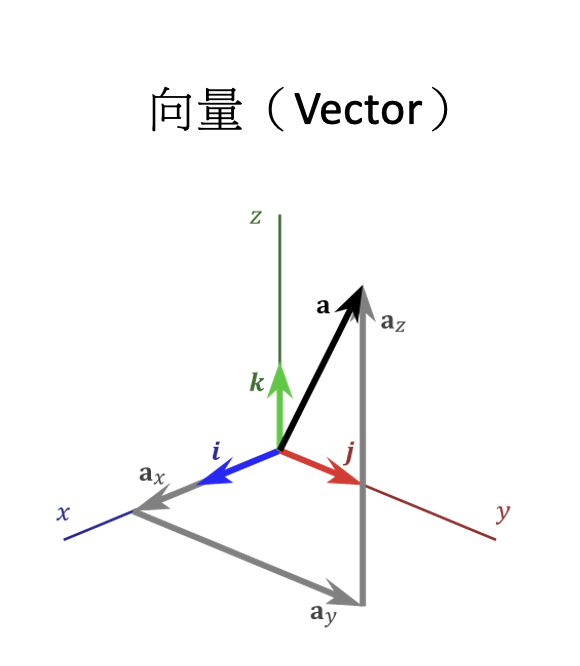
數學家：威廉·羅恩·哈密頓（William Rowan Hamilton）

發明了四元數（Quaternion）。

威廉·羅恩·哈密頓（William Rowan Hamilton）是19世紀愛爾蘭最出色的數學家之一，於1805年出生於愛爾蘭都柏林。哈密頓在年輕時就表現出了卓越的天賦和才能。他在14歲時進入都柏林三一學院（Trinity College Dublin），在那裡他學習了數學、物理學和天文學，成為了一位傑出的學者和研究者。

數學家哈密頓一生中最重要的貢獻就是他對向量（Vector）和四元數（Quaternion）的發明和研究。據說哈密頓在1843年的一次散步中，靈光一閃，想到了如何構造四元數。他在石橋上，刻下了四元數的公式：i² = j² = k² = ijk = -1。四元數是一種擴展了複數的數學結構，可以用來表示三維空間中的旋轉，並應用於物理學、機器人學、電腦圖形學等領域。

數學家：布萊茲‧帕斯卡（Blaise Pascal）

發表了帕斯卡定理（Pascal’s Theorem）。

布萊茲‧帕斯卡（Blaise Pascal）是17世紀法國最偉大的數學家之一。帕斯卡於1623年出生於克萊蒙費朗，是一位富裕的法官的兒子。他的父親對於數學和科學有著濃厚的興趣，因此在家庭教育中布萊茲早期受到了良好的培養。

他在16歲時就發表了他的第一篇數學論文，至今被稱作「帕斯卡定理」。帕斯卡定理（Pascal’s Theorem）是一條基本的射影幾何定理，它闡述了在一個圓錐曲線上任意取六個點，將它們兩兩相連，得到三條交線，這三條交線的交點共線。這個共線點被稱為帕斯卡點，它是這個圓錐曲線的一個重要特徵。

此外，數學家帕斯卡還在機械計算機的發展方面做出了貢獻，他發明了帕斯卡計算器，這是一種機械式計算器，可以進行加、減、乘、除等基本運算，並且支持重複運算。帕斯卡計算器被廣泛應用於商業和科學研究中，是現代計算機的前身。

如對於DSE數學有任何問題，如私人補習、網上補習，或者想知道更多關於DSE的資訊，歡迎Follow「學博教育中心 Learn Smart Education」 Facebook page 和 IG，以及 瀏覽 GJ MATHS 的 數學資源網站 及 IG，入面有齊所有你想知道和你需要知道的DSE資訊，助你全力應戰DSE！！

此外，臨近暑假，學博教育推出各科暑期課程，如有興趣，歡迎瀏覽 學博教育-暑期課程Page。